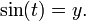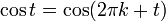* نظرية أرخميدس ..

                         

1 ـ حياته:

الاسم:أرخميدستاريخ الميلاد:287 ق.متاريخ الوفاة:212 ق.ممدرسة/نقليد فلسفي:الاهتمامات الرئيسية:{{{الاهتمامات الرئيسية}}}أفكار مميزة:هيدروستاتيكا
رافعة
موحل في الصغرتأثر ب :إقليدسحياتة :ولد أرخميدس السراقي في عام 287 ق.م في مدينة سيراكوزا Syracuses في صقلية، وهو من الأوائل الذين درسوا على يد إقليدس. و أصبحتْ نظرياتَه وفلسفتَه معروفة للعالمَ. كَسبَ سمعة ميزته عن علماءِ عصره الآخرينِ في هذه الفترةِ . ويُعتَبَرُ مِن قِبل أكثر مؤرخين الرياضياتِ كأحد علماءِ الرياضيات العظماء.

وأغلب الحقائقِ حول حياتِه ُ أخذت مِنْ السيرة الذاتية للجندي الرومانيِ مارسيلوس سجلها الرومانيِ Plutarch.

قضى أرخميدس معظم أيامهِ في مصر ، لَكنَّه إستقرَّ بقية حياتِه في مدينةسيراكوزا المدينة الرئيسية في صقلية ، إذ كان على علاقات متينة مَع ملكِها، هيروالثّاني Hieron.

نَشرَ أرخميدس أعماله على شكل مراسلةِ مَع علماءِ عصره الرئيسيينِ فيْ وقتِه، من ضمن هؤلاء العلماءِ الإسكندريينِ Conon مِنْ Samos ، وEratosthenes مِنْ Cyrene.

إن أعمالِه المعروفةِ كَانتْ نظرية، على الرغم من إهتمامه في الميكانيكا . كتب في الأعمالَ الميكانيكية والأستاتيكيةِ الموائع النظرية ِ، و لكن طريقةَ طرحه كانت تهتمُ بالنظرياتِ الميكانيكيةِ، وتدل الدراسات بأنّه غلبَ التفكير الميكانيكي واستعمله كأداة إرشادية لإكتشافِ النظرياتِ الرياضيةِ الجديدةِ.



"أعطِني مكانا لوَقْف وإراحة عتلتِي على الأرض ، وأنا أستطيع أَنْ أُحرّكَ الأرضَ."
2 ـ أعماله:
كانت المدينة التي عاش فيها أرخميدس ميناءاً بحرياً ولهذا كان موضوع الأجسام العائمة شيئاً طبيعياً له.

وننتقل الآن إلى قانون أرخميدس المشهور والموصوف في كتاب "الأجسام العائمة":
أهم أسس هذا القانون :
1-إذا غمر جسم صلباً غمراً كاملاً في سائل لايذوب فيه ولايتفاعل معه غمراً كاملاً. فإنه يخضع لقوة شاقولية مساويةُ في المقدارِ إلى قوةِ الجاذبيةِ على السائلِ المزاح.

· توازن الأثقال المختلفة على أبعاد متساوية وعدم التوازن على أبعاد غير متساوية

ونجد في كتاب أرخميدس أيضاً عدد من المصطلحات الأخرى مثل مفهوم مركز الثقل-البكرة المركبة –العتلة....الخ .

أما اكتشافه البارع فهو النسبة الثابتة ، و قانون الذراع لحساب حجم الكرة .

· البرغي الهيدروليكيِ – وهي أداة ميكانيكية لرَفْع الماءِ مِنْ مستوى منخفضُ إلى مستوى أعلى

· العتلة وهي أداة حركية يستفاد منها في رفع الأثقال ، البكرة المركبة. والمرآة المُحرقة.

كذلك كان أرخميدس عالماً في مجال البصريات، إذ توجد مقولة بأنه استخدم في الحرب ضد الأسطول الرومي مرايا مقعرة واستطاع أن يحرق السفن عن طريق تجميع الأشعة في بؤرة محددة.

ومما وصل إلينا من أعمال أرخميدس يؤكد صحة المقولة أن أرخميدس عرف جيداً المرايا المقعرة وعملها الحارق، وأجرى تجارب في انكسار الضوء، وعرف خصائص الخيال في المرايا المستوية والمقعرة والمحدبة.

ويعتبر أرخميدس قمة للأفكار العلمية في العصر القديم، وكثير من العلماء أضافوا الكثير من الأفكارإليه والتي لم تكن واضحة أثناءها لأرخميدس.

كَانَ أفضل إكتشافِ لـه تلك العلاقةِ بين السطحِ والحجم وتَحديد حجم الأسطوانة، وصياغتِه قوانين hydrostatic ويعد ذلك من أهم قوانينه الفيزيائية.
العلاقةَ بين السطحِ وحجم الأسطوانة المَحددة
وصف أرخميدس طبيعة السوائل واعتبر أن سطح أي سائل غير متحرك يملك شكلاً كروياً ومركزه يتطابق مع مركز الأرض .
في الميكانيكا إكتشفَ أرخميدس نظرياتَ أساسيةَ تَتعلّقُ بمركزِ ثقل الاجسام المستويةِ والمواد الصلبةِ.

لَعبَ أرخميدس دوراً مهماً في الدفاعِ عن سيراكوزا أثناء الحصار،ِ إذ صنع للملك هيرو أجهزة حربيةِ فعّالة جداً مما أطال فترة الحصار الروماني على سيراكوزا وأخر سقوطهاِ لمدة طويلة في 212 قبل الميلاد. لكن سيراكوزا سقطت في النهاية وأسر أرخميدس مِن قِبل الجنرالِ الرومانيِ ماركوس كلوديوس مارسيلوس في خريفِ 212 أَو ربيعِ مِنْ 211 قبل الميلاد، ومات قُتِلاًَ هناكِ. وتم نهب تلك الأجهزة والأدوات.


ويبدو أن ماخلفه أرخميدس فعلاً كان أكثر مما وصل، فقد ذكر النديم في كتابه الفهرست:" لقد أخبرني الثقة أن الروم أحرقت كتب أرشميدس خمسة عشر حملاً، وذلك خبر يطول شرحه"، ثم يعدد الكتب التي وصلت عنه، وطبقاً للعالم Plutarch، كَانَ أرخميدس لا يبدِ أي رأي في أي نوعِ من إختراعاته العمليةِ التي بَرعَ فيها لأنه لم يتَركَ أي عملِ مكتوبِ على مثل هذه المواضيعِ. بينما هو في الحقيقة غيرُ ذلك.
ومن أعمالَ أرخميدس الخالدة:
في 14 من شهر تشرين الأول عام 2000 تم إستعمال تقنيةِ حديثةِ لكَشْف الأسرارِ الموجودة في مخطوطة قديمة تعود لارخميدس ِ، حيث فك العلماءَ رموز خمسة مِنْ صفحاتِ المخطوطة المعروفةِ الوحيدةِ بنَصّ يوناني بعمر 2,300 سنةً مِن قِبل عالمِ الرياضيات أرخميدس. و يَتمنّونَ إكْمال ترجمة هذه الإطروحةِ التي تتجاوز 174 الصفحةِ، "على الأجسامِ العائِمةِ.

ويَعتقدُ العلماءُ أن الإطروحةَ نُسِختْ مِن قِبل كاتب في القرن العاشرِ مِنْ لفائفِ أرخميدس الأصلية اليونانية، إذ يتوقع أنها تَحتوي على النَصُّ الأصلي المتضمن على جذورَ حساب التفاضل والتكاملِ الحديثِ أيضاً، ونظريةِ الجاذبيةِ.

ولأرسطو(كِتابان) في التوازناتِ المستويةِ وتربيع القطع المكافىء، و(كِتابان) على السطح والإسطوانة، و(كِتابان) في اللوالبِ، على المخروط والأجسام شبه كروية، وعلى الأجسامِ العائِمةِ، وكتاب في عمل الآلة التي تطرح بالبنادق.
3 ـ أساطير حول أرخميدس:

الأسطورة الأولى: تدور حول نظريته المشهورة للطفو – التي إكتشفْها أرخميدس (مبدأ أرخميدس)- بينما كان يسْتِحْم- وكَانَ متحمّس جداً بِحيث خرج عاري إلى شوارعِ Syracuse يَصِيحُ "وجدتها، وجدتها (وَجدتُه)! ".

وتَصِفُ الأسطورةُ الأخرى: إن أرخميدس كَشفَ إحتيالاً ضدّ الملكِ Hieron الثّاني Syracuse باستخدامه مبدأَه في الطفو.وتتلخص القصة بإن الملكَ Hieron شَكَّ بأنّ تاجه الذهبي الذي طَلبهَ مخلوط بالفضةِ جزئياً.

أَخذَ أرخميدس وزنان متساويان الأول من الذهب الصافي والثاني من الفضةِ وقَارنَ أوزانَهم وذلك بتغطيسهما في الماءِ. قَارنَ الأوزانَ الناتجة مع الاوزان المركبة بنفسْ الأبعادِ المماثلةِ. ولاحظ الإختلاف بين هذه المقارنتين فاكَشتف بأنّ التاجَ ليس ذهباً صافياً.


· المضخة الأرخميدسية لرَفْع الماءِ: إخترعها َ أرخميدس لإزالة الماءِ مِنْ حوض سفينة كبيرة. وهي عبارة عن إنبوب دائري مترافقُ مع لولب يميلَ بزاوية حوالي 45 درجةَ .يُسبّبُ دورانُ هذه الألة إرتِفاع الماءَ في الإنبوبِ

وصمم مضخات البراغي الحديثةِ، التي تسمى لولب أرخميدس، وتَشْملُ اللوالبِ الَدُوراة وتستخدمُ في المنخفضاتِ المَائلةِ المفتوحةِ، وهي فعّالة لضخّ مياه المجاري وِ معالجة مياه الفضلاتِ.

شهدَ مارسيلوس لَه، بأنه كَانَ مبدعَ .

وقد صنع قبة فلكية: وهي نموذج ميكانيكي تمثل حركاتَ الشمسِ، قمر، وكواكب كما ينُظِرَ إليهامِنْ الأرضِ.

كْتبُ Cicero بأنَّ أرخميدس لا بدّ وأنه "وهب من الله عبقرية عظيمةِ جعلته قادر على بِناء مثل هذا الأداةِ التي لم يسبق لها مثيل"ِ.

وقد أشارالعديد مِنْ الكُتّابِ القدماءِ الآخرين إلى قبة أرخميدس الفلكيةِ أيضاً في أعمالهم النثرية،ِ وفي أشعارهمِ. وآخرون عدوها كبرهان للكون لا بدَّ وأنْ له خالق قدسي.

وعْكسُ Cicero الحجّة لتَأكيد ذلك بما أن الكونِ لـه خالق قدسي، يَجِبُ أَنْ يكون أرخميدس قسّاً لِكي يكون قادرًا على تَقليد حركاتِه.

وفي عام 1900 م إكتشفتْ حطام سفينة في شاطئِ الجزيرةِ اليونانيةِ لAntikythera وكَشف عنْ كنز غير متوقّعَ. السفينةغرقت في القرن الأولِ قبل الميلاد وكَانتْ تُبحرُ مِنْ الجزيرةِ اليونانيةِ Rhodes. وسط الشحنِة كَانَ هناك ترسِ في حالةٍ مُتَدهوَرة وهو أداة أرخميدس ، ما يسمى الآن بآلية Antikythera، تم تحُليّلَها في جامعةِ يايل، و إستنتجَ بأنّها كَانتَ القبة الفلكيةَ القديمةَ التي فيها مواقعَ الأجرام السماوية والتي أُشيرتْ إليها بالأوجهِ على وجهِ الأداةِ.

· إكتشافَ أرخميدس النسبة الثابتة:لخّص اقليدس براهينَ هندسيةَ عديدةَ تَستعملُ الشكل الهندسي الذي َبْرعُ أرخميدس فيه خصوصاً في استعمال حسابات المناطقِ والحجم.

، بالرغم من أنّ شهرة أرخميدس شاعت في إنجازه اختراعات ميكانيكية، فهو عالم رياضيات رائع ساعدَ على تَطوير عِلْمِ الهندسةِ. تَوقّعتْ طرقُه في حسابَ التكامل قبل 2,000 سنة من نيوتن Leibniz. بالرغم من اكتشافه العديد مِنْ أنواع الأجسامِ الصلبةِ المُشَكَّلة بانتظام مثل التي وَجدتْ عند أفلاطون المثالي نذكر منها، رباعي السطوح والمكعّب.. الخ.
4 ـ موت أرخميدس:
قُتِلَ أرخميدس في عام 212 قبل الميلاد أثناء سقوط مدينة Syracuse مِن قِبل الرومان في حربِ Punic الثانية بعد أن بذل كل جُهودِه لإبْعاد الرومان بخططه واختراعاته الحربية التيِ فَشلَ في إنجازها. وهناك رأيان حول قصّةِ قتله:

الأول : قتل أرخميدس غدراً بوساطة جندي روماني سَحبَ سيفَه وقتله بأمرمن مارسيلوس.

الثاني :عندما كان أرخميدس يوجه المرايا لاحراق السفن الرومانية ظن الجنود أنه يحمل ذهباً فوجهوا سهامهم عليه فقتلوه. ودُفِنَ حيث ماتَ في مدينة Syracuse. ونقشُ على قبرِه النسبة الثابتةِ، الاكتشاف الأكْثَر شَهْرَة. ووَضعوا أيضاً على شاهدةِ قبره إسطوانة وكتبوا عليها النسبة 2:3 نسبة الحجومِ بينهما

المثلث القائم الزاوية

للمثلث القائم الزاوية خاصية ينفرد بها عن بقية المثلثات برهنا الفيلسوف اليوناني الشهير ـ فيثاغورث ـ 580 قبل الميلاد ـ وقد عرفت باسمه رغم أنها كانت معروفة ومطبقة عمليا لدى قدماء المصريين والبابليين والهنود قبل عصر فيثاغورث نص نظرية فيثاغورث في المثلث القائم الزاوية يكون مربع طول الوتر مساويا مجموع مربعي طولي القائمة المثلث الثلاثيني الستينينتيجة :في المثلث الثلاثيني الستيني يكون طولالضلع المقابل للزاوية التي قياسها 30 ْ يساوي نصف طول الوترنظرية فيثاغورث واحدة من النظريات الاساسية في المثلثات هي نظرية فيثاغورث و التي تنص على انه في المثلث القائم، مربع طول الوتر (ا َ) يساوي الى مجموع مربعي طولي الضلعين القائمين مما يعني ان معرفة طولي ضلعين من المثلث القائم، كاف لمعرفة طول الضلع الثالث..من الممكن تعميم نظرية فيثاغورث لتشمل اي مثلث عبر قانون التجيبو هو صحيح من اجل كل المثلثات حتى و لو لم تكن قائمة يجب ملاحظة أن نظرية فيثاغورس تصلح فقط ضمن نطاق الهندسة الإقليدية.# إذا اختلف طولا ضلعين في مثلث فأكبرهما في الطول تقابله زاوية أكبر في القياس من قياس الزاوية المقابلة للآخر والعكس صحيح=================================================# إذا كان مربع طول الضلع الأطول في مثلث أصغر من مجموع مربعي طولي الضلعين الآخرين فإن المثلث حاد الزوايا =================================================# إذا كان مربع طول الضلع الأطول في مثلث أكبر من مجموع مربعي طولي الضلعين الآخرين فإن المثلث منفرج الزاوية وتكون الزاوية المنفرجة هي الزاوية المقابلة للضلع الأكبر=================================================# إذا كان مربع طول الضلع الأطول في مثلث مساويا لمجموع مربعي طولي الضلعين الآخرين فإن المثلث قائم الزاوية وتكون الزاوية القائمة هي الزاوية المقابلة للضلع الأكبر (( عكس نظرية فيثاغورث ))

نظرية فيثاغورس

للمثلث القائم الزاوية خاصية ينفرد بها عن بقية المثلثات برهنا الفيلسوف اليوناني الشهير ـ فيثاغورث ـ 580 قبل الميلاد ـ وقد عرفت باسمه رغم أنها

كانت معروفة ومطبقة عمليا لدى قدماء المصريين والبابليين والهنود قبل عصر فيثاغورث

نص نظرية فيثاغورث

في المثلث القائم الزاوية يكون مربع طول الوتر مساويا مجموع مربعي طولي القائمة

المثلث الثلاثيني الستيني




نتيجة :
في المثلث الثلاثيني الستيني يكون طول
الضلع المقابل للزاوية التي قياسها 30 ْ
يساوي نصف طول الوتر


نظرية فيثاغورث واحدة من النظريات الاساسية في المثلثات هي نظرية فيثاغورث و التي تنص على انه في المثلث القائم،
مربع طول الوتر (ا َ) يساوي الى مجموع مربعي طولي الضلعين القائمين


مما يعني ان معرفة طولي ضلعين من المثلث القائم، كاف لمعرفة طول الضلع الثالث..

من الممكن تعميم نظرية فيثاغورث لتشمل اي مثلث عبر قانون التجيب

و هو صحيح من اجل كل المثلثات حتى و لو لم تكن قائمة

يجب ملاحظة أن نظرية فيثاغورس تصلح فقط ضمن نطاق الهندسة الإقليدية.





# إذا اختلف طولا ضلعين في مثلث فأكبرهما في الطول تقابله زاوية أكبر في القياس من قياس الزاوية المقابلة للآخر والعكس صحيح

=================================================
# إذا كان مربع طول الضلع الأطول في مثلث أصغر من مجموع مربعي طولي الضلعين الآخرين فإن المثلث حاد الزوايا

=================================================
# إذا كان مربع طول الضلع الأطول في مثلث أكبر من مجموع مربعي طولي الضلعين الآخرين فإن المثلث منفرج الزاوية وتكون الزاوية المنفرجة هي الزاوية المقابلة للضلع الأكبر

=================================================
# إذا كان مربع طول الضلع الأطول في مثلث مساويا لمجموع مربعي طولي الضلعين الآخرين فإن المثلث قائم الزاوية وتكون الزاوية القائمة هي الزاوية المقابلة للضلع الأكبر (( عكس نظرية فيثاغورث ))

دائرة الوحدة

دائرة وحدة

 

دائرة الوحدة.

في الرياضيات، الدائرة الوحدة هي دائرة نصف قطرها يساوي الواحد.
تستخدم هذه الدائرة في حساب المثلثات حيث يكون مركزها يقع في نقطة المبدأ لنظام الإحداثيات الديكارتية، وطول نصف قطرها يساوي الواحد. يرمز لدائرة الوحدة في المستوي الإقليدي بالرمز S¹　والتعميم لأبعاد أعلى ينتج كرة الوحدة.

* التوابع المثلثية على دائرة الوحدة

من الممكن تعريف التوابع المثلثية على دائرة وحدة على الشكل التالي:
إذا كانت النقطة (x, y) هي نقطة على دائرة الوحدة، وكان الشعاع الذي مبدأ النقطة (0, 0) إلى النقطة (x, y) تشكل زاوية t مع محور x الموجب (حيث الاتجاه الموجب هو اتجاه عكس عقارب الساعة) عندها يكون:

وبما أن في الدائرة الواحدية
x² + y² = 1 ينتج لدينا العلاقة

لاحظ أن cos²(t)=(cos(t))².
وتساعد الدائرة الواحدية على إدرام ان تابع الجيب وتابع جيب التمام هي توابع دورية بالشكل

من أجل أي قيمة للعدد الصحيح　K.

دوال مثلثية

 

اذهب إلى: تصفح, البحث

في الرياضيات، تعتبر التوابع المثلثية أو الدوال المثلثية دوال لزاوية هندسية، وهي دوال مهمة عندما نريد دراسة مثلث أوعرض ظواهرِ دورية. يمكن تعريف هذه الدوال ك نسبة لأضلاع مثلث قائم الذي يَحتوي تلك الزاويةَ أَو بشكل أكثر عمومية كإحداثيات على دائرة مثلثية أو دائرة واحدية unit circle.
في الرياضيات، الدوال المثلثية هي دوال ترتبط بالزاوية، وهي مهمة في دراسة المثلثات وتمثيل الظواهر المتكررة (كالموجات). ويمكن تعريف الدوال المثلثية على أنهم نسب بين ضلعين في مثلث قائم فيه الزاوية المعنية، أو، وبشكل أوسع. كنسبة بين إحداثيات نقاط على دائرة الوحدة، ويعتبر دوما عند الإشارة إلى المثلثات ان الحديث يدور حول مثلث في سطح مستوي (مستوى إحداثي أو إقليدي)، وذلك ليكون مجموع الزوايا 180 درجة دائما.

محتويات 1 أنواع الدوال المثلثية 2 علاقات مثلثية 2.1 تمثيل بياني لدالة جيب التمام 2.2 تمثيل بياني لدالة الجيب 3 إنظر أيضا

* أنواع الدوال المثلثية

توجد ثلاثة دوال مثلثية أساسية هي:

• جا أو الجيب، ويساوي النسبة بين الضلع المقابل للزاوية مقسوما على الوتر.
• جتا أو جيب التمام، ويساوي النسبة بين الضلع المجاور للزاوية مقسوما على الوتر.
• ظا أو الظل، ويساوي النسبية بين الضلع المقابل للزاوية والضلع المجاور لها.

اسم التابع	الاختصار	العلاقة
جيب	sin أو جب أو جا
تجيب أو جيب تمام	cos، تجب أو جتا
ظل	tan، ظل أو ظا
تظل أو ظل تمام	cot، تظل أو ظتا
Secantأو قاطع	sec أو قا
Cosecant أو قاطع تمام	csc أو قتا

* علاقات مثلثية

* تمثيل بياني لدالة جيب التمام

*  تمثيل بياني لدالة الجيب

مخترع الألة الحاسبة .. بليز باسكال ..

بليز باسكال

تمثال لباسكال وهو يدرس المتدحرج cycloid قام بعمله أوغستين باجو عام 1785، محفوظ في متحف اللوفر

باسكال، بليز "Blaise Pascal"؛ (19 يونيو 1623 - 19 أغسطس 1662)، فيزيائي ورياضي وفيلسوف فرنسي اشتهر بتجاربه على السوائل في مجال الفيزياء، وبأعماله الخاصة بنظرية الاحتمالات في الرياضيات هو من اخترع الآلة الحاسبة. استطاع باسكال أن يسهم في إيجاد أسلوب جديد في النثر الفرنسي بمجموعته الرسائل الريفيّة.
أدَّت أعمال باسكال المهمة في مجال ضغط السوائل إلى إيجاد المبدأ المسمى قانون باسكال، الذي ظهر خلال الخمسينيات من القرن السابع عشر الميلادي. وينص هذا المبدأ على أن السوائل الموجودة في الأوعية تنقل ضغوطًا متساوية في كافة الجهات، كما يوضح العمليات التي تقوم بها ضاغطات الهواء، والمضخات الفراغية، والرافعات الهيدروليكية، ورافعات السيارات، والمضاغط. ساعدت تجارب باسكال على إثبات أن للهواء وزناً، وأن ضغط الهواء يمكن أن ينتج فراغًا، وبذلك أزال شكوك العلماء في ذلك الوقت في إمكان وجود الفراغ.
وخلال الخمسينيات من القرن السابع عشر الميلادي قدم باسكال، وعالم الرياضيات الفرنسي بيير دي فيرمات نظرية الاحتمالات، وناقشا بعض تطبيقاتها. وصمم باسكال عام 1654م تنظيمًا ثلاثيًا من الأرقام يكون فيه كل رقم مساويًا لمجموع الرقمين المجاورين له من جهة اليمين، وعلى جانبه الأيسر في الصف الذي يكون أعلاه مباشرة. ويمكن استخدام هذا التنظيم الذي سمِّي مثلث باسكال في حساب الاحتمالات. انظر: التباديل والتوافيق. واخترع باسكال أيضًا آلة حاسبة تؤدي عمليات الجمع والضرب.

محتويات (الفهرس )  1 حياته 2 الهندسة الرياضية عند باسكال 3 إنجازاته 3.1 التحليل المتناهي الصغر 3.2 في الحساب 3.3 في الاحتمالات 3.4 الآلة الحاسبة

*  حياته

وُلد باسكال في مدينة كلير مونت ـ فيراند بفرنسا. وقد أظهر نبوغا في الرياضيات منذ أن كان طفلاً. واشتغل في حركة دينية تسمى الجانسينية، وفي أواخر عام 1654م دخل ديرًا من أديرة هذه الجماعة في مدينة بورت ـ رويال. وقد اتهمت المنظمة اليسوعية الجانسينيين بالبدعة، وأدانت قائدهم أنطوني آرنولد. وردًا على هذا الاتهام قام باسكال فورًا بنشر 18 كتيبًا ساخرًا سميت الرسائل الريفية، وقد لاقت شعبية عظيمة في عامي 1656 و 1657م.
ظل باسكال يدافع منذ عام 1658م وحتى وفاته عن عقيدته. وقد وُجدت بعض أجزاء من عمله هذا الذي لم يكن قد اكتمل في ذلك الوقت بعد وفاته، وطبع باسم بنسيز. ويعبر هذا العمل عن إيمان باسكال بأن هناك حدودًا للحقائق التي يمكن أن يدركها العقل، وأن الإيمان من القلب بالرسالة المسيحية هو المرشد الرئيسي إلى الحقائق.

* الهندسة الرياضية عند باسكال

فيما عدا الهندسة المتناهية الصغر عالج باسكال الهندسة الإسقاطية كما تناول المخروطيات les coniques وبعدها القطاعات المخروطية. بدأ الاهتمام بالهندسة من عمر الثانية عشرة عندما قرأ كتاب العناصر لأقليدس. وأكمل اهتمامه بشكل رصين منذ السنة 1639 بالنسبة للدائرة، المخروط، الكرة، الأمكنة الهندسية لنقطة متغيرة. لكن الهندسة التحليلية التي عالجها ديكارت لم يهتم بها باسكال مطلقا.
لكن عمل باسكال الهندسة لم ينل إعجابا في عصره، فقد بقي حتى القرن التاسع عشر حين جاء بننسيليه Poncelet فأظهر أهمية باسكال.

( إنجازاته)

*  التحليل المتناهي الصغر

كانت له مكإنة عظيمة في هذا الميدان، وقد نشر باسكال أعماله في هذا المجال بين سنة 1650 و 1660 أي في آخر سني حياته، اعتمد قليلا على ستيفن، ودي كارت، وروبرفال، وتورتشللي وغيرهم. لكنه سبق نيوتن، وليبنتز، الذين أخذوا عنه أشياء كثيرة، كما تناول مفهوم الحدود، ومرائل التكامل ومفهوم المثلث المميز المعروف باسمه Triangle de Pascal>/O:P>
قام باسكال بتطبيق كل هذه الأساليب في مسائل عديدة في الرياضيات حينا وفي الفيزياء والميكانيك حينا آخر.

*  في الحساب

مثلث باسكال

.
اهتم بخصائص السلاسل العددية الصحيحة وبالترتيب العددي والأعداد الطبيعية والأعداد المثلثية، ومثلث باسكال وتطبيقاته العديدة.

* في الاحتمالات

يمكننا عن حق القول بأن باسكال هو الذي أسس حساب الاحتمالات. كان هناك احتمالات الألعاب وبعض أنواع التجارة وما شابه إنما لم يكن هناك علم بالمعنى الصحيح يرتكز إلى أصول الرياضيات.

*  الآلة الحاسبة

إحدى أوائل آلات باسكال الحاسبة

تعتبر هذه الآلة إحدى أوجه تقدم العلوم التطبيقية. إنها فعلا اكتشاف جدير بالاهتمام، فهو الذي أوصل الإنسانية إلى الحاسبات الحديثة وما يمكن أن تصل إليه في المستقبل. فقد اكتشفها في روان Rouen سنة 1640 وهي آلة تقوم بإجراء للعمليات الحسابية الأربع دون جهد في التفكير وذلك لتأدية حسابات والده بسرعة.إن عملية مكننة الحساب تعتبر خطوة جبارة على طريق الحضارة الإنسان