دوال مثلثية
في الرياضيات، تعتبر التوابع المثلثية أو الدوال المثلثية دوال لزاوية هندسية، وهي دوال مهمة عندما نريد دراسة مثلث أوعرض ظواهرِ دورية. يمكن تعريف هذه الدوال ك نسبة لأضلاع مثلث قائم الذي يَحتوي تلك الزاويةَ أَو بشكل أكثر عمومية كإحداثيات على دائرة مثلثية أو دائرة واحدية unit circle.
في الرياضيات، الدوال المثلثية هي دوال ترتبط بالزاوية، وهي مهمة في دراسة المثلثات وتمثيل الظواهر المتكررة (كالموجات). ويمكن تعريف الدوال المثلثية على أنهم نسب بين ضلعين في مثلث قائم فيه الزاوية المعنية، أو، وبشكل أوسع. كنسبة بين إحداثيات نقاط على دائرة الوحدة، ويعتبر دوما عند الإشارة إلى المثلثات ان الحديث يدور حول مثلث في سطح مستوي (مستوى إحداثي أو إقليدي)، وذلك ليكون مجموع الزوايا 180 درجة دائما.
محتويات |
* أنواع الدوال المثلثية
توجد ثلاثة دوال مثلثية أساسية هي:- جا أو الجيب، ويساوي النسبة بين الضلع المقابل للزاوية مقسوما على الوتر.
- جتا أو جيب التمام، ويساوي النسبة بين الضلع المجاور للزاوية مقسوما على الوتر.
- ظا أو الظل، ويساوي النسبية بين الضلع المقابل للزاوية والضلع المجاور لها.
| اسم التابع | الاختصار | العلاقة |
| جيب | sin أو جب أو جا |  |
| تجيب أو جيب تمام | cos، تجب أو جتا |  |
| ظل | tan، ظل أو ظا |  |
| تظل أو ظل تمام | cot، تظل أو ظتا |  |
| Secantأو قاطع | sec أو قا  | |
| Cosecant أو قاطع تمام | csc أو قتا |  |
* علاقات مثلثية


* تمثيل بياني لدالة جيب التمام

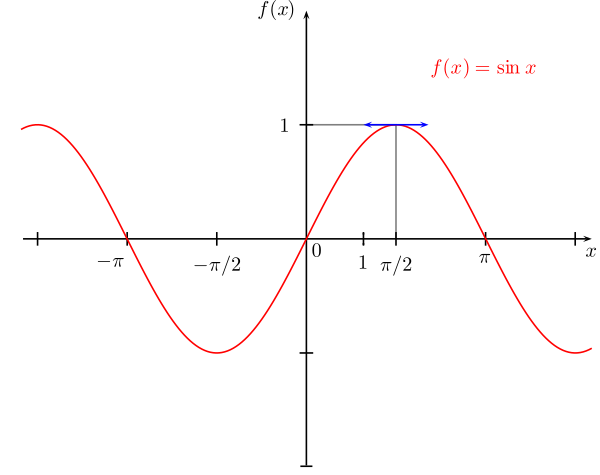
* تمثيل بياني لدالة الجيب


شكرا
ردحذف